GRADIENTE, ROTACIONAL Y DIVERGENCIA
Gradiente


En esta imagen, el campo escalar se aprecia en blanco y negro, representando valores bajos o altos respectivamente, y el gradientecorrespondiente se aprecia por flechas azules.
El gradiente normalmente denota una dirección en el espacio según la cual se aprecia una variación de una determinada propiedad o magnitud física.
En otros contextos se usa informalmente gradiente, para indicar la existencia de gradualidad o variación gradual en determinado aspecto, no necesariamente relacionado con la distribución física de una determinada magnitud o propiedad.
//
Definición
El gradiente de un campo escalar, que sea diferenciable en el entorno de un punto, es un vector definido como el único que permite hallar la derivada direccional en cualquier dirección como:

siendo
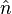 un vector unitario y
un vector unitario y  la derivada direccional de
la derivada direccional de 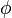 en la dirección de
en la dirección de 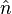 , que informa de la tasa de variación del campo escalar al desplazarnos según esta dirección:
, que informa de la tasa de variación del campo escalar al desplazarnos según esta dirección:
Una forma equivalente de definir el gradiente es como el único vector que, multiplicado por cualquier desplazamiento infinitesimal, da el diferencial del campo escalar:

Con la definición anterior, el gradiente está caracterizado de forma unívoca. El gradiente se expresa alternativamente mediante el uso del operador nabla:

Interpretación del Gradiente
De forma geométrica el gradiente es un vector que se encuentra normal a una superficie o curva en el espacio a la cual se le esta estudiando, en un punto cualquiera, llamese
 ,
,  ,
,  etcétera. Algunos ejemplos son:
etcétera. Algunos ejemplos son: Considere una habitación en la cual la temperatura se define a través de un campo escalar, de tal manera que en cualquier punto
 , la temperatura es
, la temperatura es  . Asumiremos que la temperatura no varia con respecto al tiempo. Siendo esto así, para cada punto de la habitación, el gradiente en ese punto nos dará la dirección en la cual se calienta más rápido. La magnitud del gradiente nos dirá cuán rápido se calienta en esa dirección.
. Asumiremos que la temperatura no varia con respecto al tiempo. Siendo esto así, para cada punto de la habitación, el gradiente en ese punto nos dará la dirección en la cual se calienta más rápido. La magnitud del gradiente nos dirá cuán rápido se calienta en esa dirección. Considere una montaña en la cual su altura en el punto
 se define como
se define como  . El gradiente de H en ese punto estará en la dirección para la que hay un mayor grado de inclinación. La magnitud del gradiente nos mostrará cuán empinada se encuentra la pendiente.
. El gradiente de H en ese punto estará en la dirección para la que hay un mayor grado de inclinación. La magnitud del gradiente nos mostrará cuán empinada se encuentra la pendiente. Aproximación lineal de una función
El gradiente de una función f definida de Rn a R caracteriza la mejor aproximación lineal de la función en un punto particular x0 en Rn. Se expresa así:

donde
 es el gradiente evaluado en x0.
es el gradiente evaluado en x0.Propiedades
El gradiente verifica que:
Es ortogonal a las superficies equiescalares, definidas por
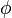 =cte..
=cte.. Apunta en la dirección en que la derivada direccional es máxima.
Su módulo es igual a esta derivada direccional máxima.
Se anula en los puntos estacionarios (máximos, mínimos y puntos de silla)
El campo formado por el gradiente en cada punto es siempre irrotacional, esto es,

Expresión en diferentes sistemas de coordenadas
A partir de su definición puede hallarse su expresión en diferentes sistemas de coordenadas.
En coordenadas cartesianas, su expresión es simplemente

En un sistema de coordenadas ortogonales, el gradiente requiere los factores de escala, mediante la expresión

Para coordenadas cilíndricas (hρ = hz = 1,
 ) resulta
) resulta
y para coordenadas esféricas (hr = 1, hθ = r,
 )
)
Gradiente de un campo vectorial
En un espacio euclídeo, el concepto de gradiente también puede extenderse al caso de un campo vectorial, siendo el gradiente de
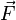 un tensor que da el diferencial del campo al realizar un desplazamiento
un tensor que da el diferencial del campo al realizar un desplazamiento
Este tensor podrá representarse por una matriz
 , que en coordenadas cartesianas está formada por las tres derivadas parciales de las tres componentes del campo vectorial.
, que en coordenadas cartesianas está formada por las tres derivadas parciales de las tres componentes del campo vectorial.Ejemplo [editar]
Dada la función f(x,y,z) = 2x + 3y2 − sin(z) su vector gradiente es:

Aplicaciones en física
El Gradiente posee innumerables aplicaciones en física, especialmente en electromagnetismo y mecánica de fluidos. En particular, existen muchos campos vectoriales que puede escribirse como el gradiente de un potencial escalar.
Uno de ellos es el campo electrostático, que deriva del potencial eléctrico

Todo campo que pueda escribirse como el gradiente de un campo escalar, se denomina potencial, conservativo o irrotacional. Así, una fuerza conservativa deriva de la energía potencial como

Los gradientes también aparecen en los procesos de difusión que verifican la ley de Fick o la ley de Fourier para la temperatura. Así, por ejemplo, el flujo de calor en un material es proporcional al gradiente de temperaturas

siendo k la conductividad térmica.
Divergencia
La divergencia de un campo vectorial mide la diferencia entre el flujo entrante y el flujo saliente de un campo vectorial sobre la superficie que rodea a un volumen de control, por tanto, si el campo tiene "fuentes" o "sumideros" la divergencia de dicho campo será diferente de cero.
//
Divergencia de un campo vectorial
La divergencia de un campo vectorial es un campo escalar, y se define como el flujo del campo vectorial por unidad de volumen:

donde S es una superficie cerrada que se reduce a un punto en el límite. El símbolo
 representa el operador nabla.
representa el operador nabla.Esta definición está directamente relacionada con el concepto de flujo del campo. Como en el caso del flujo, si la divergencia en un punto es positiva, se dice que el campo posee manantiales. Si la divergencia es negativa, se dice que tiene sumideros. El ejemplo más característico lo dan las cargas eléctricas, que dan la divergencia del campo eléctrico, siendo las cargas positivas manantiales y las negativas sumideros del campo eléctrico.
Se llaman fuentes escalares del campo
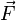 al campo escalar que se obtiene a partir de la divergencia de
al campo escalar que se obtiene a partir de la divergencia de 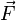

La divergencia de un campo vectorial se relaciona con el flujo a través del teorema de Gauss o teorema de la divergencia.
Coordenadas cartesianas
Cuando la definición de divergencia se aplica al caso de un campo expresado en coordenadas cartesianas,

el resultado es sencillo:
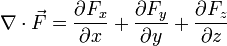
Coordenadas ortogonales
Sin embargo, para un caso más general de coordenadas ortogonales curvilíneas, como las cilíndricas o las esféricas, la expresión se complica debido a la dependencia de los vectores de la base con la posición. La expresión para un sistema de coordenadas ortogonales es:
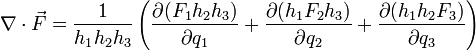
Donde los
 son los factores de escala del sistema de coordenadas, relacionados con la forma del tensor métrico en dicho sistema de coordenadas. Esta fórmula general, para el caso de coordenadas cartesianas (hx = hy = hz = 1) se reduce a la expresión anterior. Para coordenadas cilíndricas (
son los factores de escala del sistema de coordenadas, relacionados con la forma del tensor métrico en dicho sistema de coordenadas. Esta fórmula general, para el caso de coordenadas cartesianas (hx = hy = hz = 1) se reduce a la expresión anterior. Para coordenadas cilíndricas (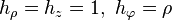 ) resulta:
) resulta:
Para coordenadas esféricas (
 ) resulta
) resulta
Coordenadas generales
En sistemas de coordenadas generales, no necesarimente ortogonales, la divergencia de un vector puede expresarse en términos de las derivadas parciales respecto a las coordenadas y el determinante del tensor métrico:

Divergencia de un campo tensorial
El concepto de divergencia puede extenderse a un campo tensorial de orden superior. En una variedad de Riemann la divergencia de un tensor T completamente simétrico
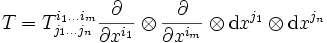
Se define como:

Por ejemplo, en teoría de la relatividad especial la energía de un sistema se representa por un tensor simétrico de segundo orden, cuya divergencia es cero. De hecho el principio de conservación de la energía relativista toma la forma:
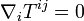
 diferenciable definida sobre un conjunto
diferenciable definida sobre un conjunto 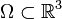 y sea
y sea  un conjunto cerrado limitado por una frontera
un conjunto cerrado limitado por una frontera  o superficie de contorno (que sea una variedad diferenciable) y sea
o superficie de contorno (que sea una variedad diferenciable) y sea 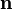 el vector normal en cada punto de la superficie, entonces se cumple que:
el vector normal en cada punto de la superficie, entonces se cumple que:

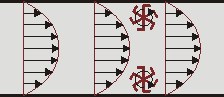
 , que se obtiene calculando el rotacional de un campo
, que se obtiene calculando el rotacional de un campo  en cada punto,
en cada punto,
 (siendo las fuentes escalares las que se obtienen mediante la divergencia).
(siendo las fuentes escalares las que se obtienen mediante la divergencia).

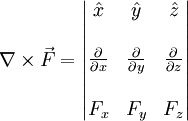



 . Sin embargo, puesto que los bivectores generalmente se consideran menos intuitivos que los vectores ordinarios, el R³-dual se utiliza comúnmente en lugar de otro: esto es una operación quiral, produciendo un pseudovector que adquiere valores opuestos en conjuntos coordenados izquierdos y derechos.
. Sin embargo, puesto que los bivectores generalmente se consideran menos intuitivos que los vectores ordinarios, el R³-dual se utiliza comúnmente en lugar de otro: esto es una operación quiral, produciendo un pseudovector que adquiere valores opuestos en conjuntos coordenados izquierdos y derechos.


Comentarios
Publicar un comentario